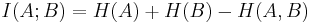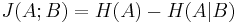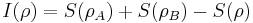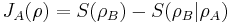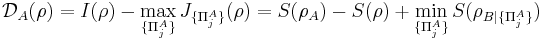Quantum discord
In quantum information theory, quantum discord is a measure of nonclassical correlations between two subsystems of a quantum system. It includes correlations that are due to quantum physical effects but do not necessarily involve quantum entanglement.
The notion of quantum discord was introduced in 2001 by Harold Ollivier and Wojciech H. Zurek[1] and, independently,[2] by L. Henderson and Vlatko Vedral.[3] Olliver and Zurek referred to it also as a measure of quantumness of correlations.[1] From the work of these two research groups it follows that quantum correlations can be present in certain mixed separable states;[4] In other words, separability alone does not imply the absence of quantum effects. The notion of quantum discord thus goes beyond the distinction which had been made earlier between entangled versus separable (non-entangled) quantum states.
Contents |
Definition and mathematical relations
In mathematical terms, quantum discord is defined in terms of the quantum mutual information. More specifically, quantum discord is the difference between two expressions which each, in the classical limit, represent the mutual information. These two expressions are:
where, in the classical case, 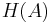 is the information entropy,
is the information entropy, 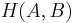 the joint entropy and
the joint entropy and 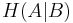 the conditional entropy, and the two expressions yield identical results. In the nonclassical case, the quantum physics analogy for the three terms are used –
the conditional entropy, and the two expressions yield identical results. In the nonclassical case, the quantum physics analogy for the three terms are used – 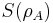 the von Neumann entropy,
the von Neumann entropy, 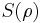 the joint quantum entropy and
the joint quantum entropy and 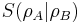 the conditional quantum entropy, respectively, for probability density function
the conditional quantum entropy, respectively, for probability density function 
The difference between the two expressions 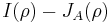 defines the basis-dependent quantum discord, which is asymmetrical in the sense that
defines the basis-dependent quantum discord, which is asymmetrical in the sense that 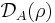 can differ from
can differ from 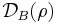 .[5][6]
.[5][6]  represents the part of the correlations that can be attributed to classical correlations and varies in dependence on the chosen eigenbasis; therefore, in order for the quantum discord to reflect the purely nonclassical correlations independently of basis, it is necessary that
represents the part of the correlations that can be attributed to classical correlations and varies in dependence on the chosen eigenbasis; therefore, in order for the quantum discord to reflect the purely nonclassical correlations independently of basis, it is necessary that  first be maximized over the set of all possible projective measurements onto the eigenbasis:[7]
first be maximized over the set of all possible projective measurements onto the eigenbasis:[7]
Nonzero quantum discord indicates the presence of correlations that are due to noncommutativity of quantum operators.[8] For pure states, the quantum discord becomes a measure of quantum entanglement,[9] more specifically, in that case it equals the entropy of entanglement.[4]
Vanishing quantum discord is a criterion for the pointer states, which constitute preferred effectively classical states of a system.[1] It could be shown that quantum discord must be non-negative and that states with vanishing quantum discord can in fact be identified with pointer states.[10] Other conditions have been identified which can be seen in analogy to the Peres–Horodecki criterion[11] and in relation to the strong subadditivity of the von Neumann entropy.[12]
Efforts have been made to extend the definition of quantum discord to continuous variable systems, in particular to bipartite systems described by Gaussian states.[4]
Properties
Quantum discord has been given a physical interpretation, in operational terms, as an “entanglement consumption in an extended quantum state merging protocol”.[12][13] Providing evidence for non-entanglement quantum correlations normally involves elaborate quantum tomography methods; however, in 2011, such correlations could be demonstrated experimentally in a room temperature nuclear magnetic resonance system, using chloroform molecules that represent a two-qubit quantum system.[14][15]
Quantum discord has been seen as a possible basis for the performance in terms of quantum computation ascribed to certain mixed-state quantum systems,[2] with a mixed quantum state representing a statistical ensemble of pure states (see quantum statistical mechanics).
Evidence has been provided for poignant differences between the properties of quantum entanglement and quantum discord. It has been shown that quantum discord is more resilient to dissipative environments than is quantum entanglement. This has been shown for Markovian environments as well as for non-Markovian environments based on a comparison of the dynamics of discord with that of concurrence, where discord has proven to be more robust.[16] It has been shown that, at least for certain models of a qubit pair which is in thermal equilibrium and form an open quantum system in contact with a heat bath, the quantum discord increases with temperature in certain temperature ranges, thus displaying a behaviour that is quite in contrast with that of entanglement, and that furthermore, surprisingly, the classical correlation actually decreases as the quantum discord increases.[17] Nonzero quantum discord can persist even in the limit of one of the subsystems undergoing an infinite acceleration, whereas under this condition the quantum entanglement drops to zero due to the Unruh effect.[18]
Alternative measures
Other measures of nonclassical correlations include the measurement induced disturbance (MID) measure and the localized noneffective unitary (LNU) distance[19] and various entropy-based measures.[20]
References
- ^ a b c Harold Ollivier and Wojciech H. Zurek, Quantum Discord: A Measure of the Quantumness of Correlations, Physics Review Letters vol. 88, 017901 (2001) abstract
- ^ a b Animesh Datta, Anil Shaji, Carlton M. Caves: Quantum discord and the power of one qubit, arXiv:0709.0548v1 [quant-ph], 4 Sep 2007, p. 1
- ^ L. Henderson and V. Vedral: Classical, quantum and total correlations, Journal of Physics A 34, 6899 (2001), DOI: 10.1088/0305-4470/34/35/315 [1]
- ^ a b c Paolo Giorda, Matteo G. A. Paris: Gaussian quantum discord, quant-ph arXiv:1003.3207v2 (submitted on 16 Mar 2010, version of 22 March 2010) p. 1
- ^ Borivoje Dakic, Vlatko Vedral, Caslav Brukner: Necessary and sufficient condition for nonzero quantum discord, arXiv:1004.0190v2 (submitted 1 April 2010, version of 3 November 2010)
- ^ For a succinct overview see for ex arXiv:0809.1723v2
- ^ For a more detailed overview see for ex. Signatures of nonclassicality in mixed-state quantum computation, Physical Review A vol. 79, 042325 (2009), DOI: 10.1103/PhysRevA.79.042325 arXiv:0811.4003 and see for ex. Wojciech H. Zurek: Decoherence and the transition from quantum to classical - revisited, p. 11
- ^ Shunlong Luo: Quantum discord for two-qubit systems, Physical Review A, vol. 77, 042303 (2008) abstract
- ^ Animesh Datta, Anil Shaji, Carlton M. Caves: Quantum discord and the power of one qubit, arXiv:0709.0548v1 [quant-ph], 4 Sep 2007, p. 4
- ^ Animesh Datta: A condition for the nullity of quantum discord, arXiv:1003.5256v2
- ^ Bogna Bylicka, Dariusz Chru´sci´nski: Witnessing quantum discord in 2 x N systems, arXiv:1004.0434v1 [quant-ph], 3 April 2010
- ^ a b Vaibhav Madhok, Animesh Datta: Role of quantum discord in quantum communication arXiv:1107.0994v1, (submitted 5 July 2011)
- ^ D. Cavalcanti, L. Aolita, S. Boixo, K. Modi, M. Piani, A. Winter: Operational interpretations of quantum discord, quant-ph, arXiv:1008.3205
- ^ R. Auccaise, J. Maziero, L. C. Céleri, D. O. Soares-Pinto, E. R. deAzevedo, T. J. Bonagamba, R. S. Sarthour, I. S. Oliveira, R. M. Serra: Experimentally Witnessing the Quantumness of Correlations, Physics Review Letters, vol. 107, 070501 (2011) abstract (arXiv:1104.1596)
- ^ Miranda Marquit: Quantum correlations – without entanglement, PhysOrg, August 24, 2011
- ^ See [2] as well as [3] and citations therein
- ^ T. Werlang, G. Rigolin: Thermal and magnetic discord in Heisenberg models, Physical Review A, vol. 81, no. 4 (044101) (2010), DOI: 10.1103/PhysRevA.81.044101 abstract, fulltext (arXiv)
- ^ Animesh Datta: Quantum discord between relatively accelerated observers, arXiv:0905.3301v1 [quant-ph] 20 May 2009, [4]
- ^ see for ex.: Animesh Datta, Sevag Gharibian: Signatures of non-classicality in mixed-state quantum computation, Physical Review A vol. 79, 042325 (2009) abstract, arXiv:0811.4003
- ^ Matthias Lang, Anil Shaji, Carlton Caves: Entropic measures of nonclassical correlations, American Physical Society, APS March Meeting 2011, March 21–25, 2011, abstract #X29.007, arXiv:1105.4920